In the last post, we implemented a parser that generates an abstract syntax tree. We will traverse the syntax tree to return our result in this final post of the series. The finish line beckons!

Interpreter 🔗

In the first post of this series, I mentioned that our program includes three main components: Scan -> Parse -> Interpret. As each of these steps is implemented, a critical goal is to ensure that the data produced by one component is easy to process in the next component.

In the Scan phase, we produced tokens. Then, we processed those tokens in the Parse phase to create an abstract syntax tree (AST). Now, in the Interpret phase, we will evaluate the AST returned by the parser to generate a final value for our program.

Using the parser we built in the last post, we can generate an AST for 120 + 12.3 * 53 - 9 that can be visualized as follows:

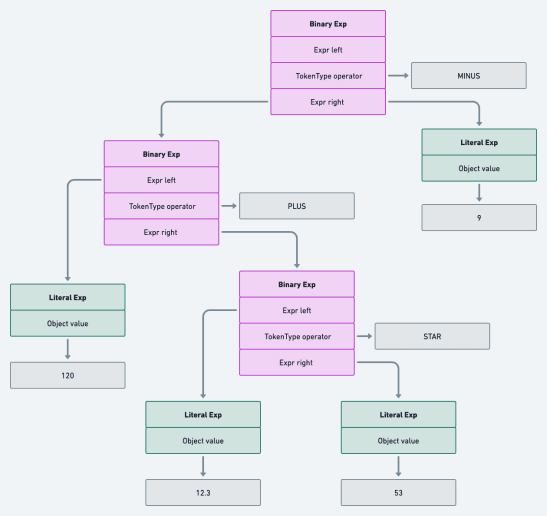
See full image here .

Using our understanding of precedence and math operations, we know that we should evaluate 12.3 * 53 first to get 651.9. Next, we add 651.9 to 120 to get 771.9. Finally, we subtract 9 from 771.9 to get 762.9, the final answer.

Looking carefully at the AST, we follow these exact sequence of steps using a post-order traversal. So, our main goal in this post is to discuss the best way to implement an interpreter that uses post-order traversal.

We’ll discuss three implementations: One using Object-oriented programming, another using functional programming concepts, and a final implementation that uses a design pattern.

Let’s go.

An Object-Oriented Interpreter 🔗

To implement the interpreter using OOP, we first define Expr - an abstract class representing all types of expressions in explanck’s grammar. Then, within Expr, we create a class for each kind of expression: Binary, Grouping, and Literal.

abstract class Expr {
	abstract Object evaluate();
	
	class Binary extends Expr {
		Binary(Expr left, Token operator, Expr right){}
		Object evaluate(){}
	}

	class Grouping extends Expr {
		Grouping(Expr expr){}
		Object evaluate(){}
	}

	class Literal extends Expr {
		Literal(Object value)P{}
		Object evaluate(){}
	}
}

Next, we define an Interpreter class that evaluates an expression by calling its evaluate() method.

class Interpreter {
	String interpret(Expr expr){
		Object value = evaluate(expr);
		return value.toString();
	}
	
	private Object evaluate(Expr expr) {
		return expr.evaluate();
	}
}

This implementation is textbook OOP - we combine our expression data and the methods that operate on them into their respective classes.

Then, when we call the interpreter with our AST (Expr expr), the runtime will know the right evaluate() method to call using polymorphism. So this implementation will work, but we have a philosophical problem here, in my opinion.

Imagine for a second that we wanted to pretty-print and type-check an AST. We’d create classes like:

class ASTPrinter {
	void print(Expr expr){
		sout(print(expr));
	}
	
	String print(Expr expr) {
		return expr.print()
	}
}

class TypeChecker{
	boolean check(Expr expr){
		return expr.check();
	}
}

Remember that for Interpreter we needed to implement evaluate() for each type of expression. So, for both ASTPrinter and TypeChecker, we’ll need to implement print() and check() respectively in every expression class.

This means that every new functionality we [potentially] provide to Explanck will require implementing a method in every expression class every time. Further, it also means that we couple multiple methods from different domains together in the same class, violating the Separation of Concerns (SoC) principle.

The primary objective of SoC is to make code modular and easy to maintain. Here, we blur the lines of concerns by mixing interpreting, printing and type-checking into each expression’s class. This violation will make the code harder to test and maintain.

Interpreting, Functionally. 🔗

A second implementation is to use ideas from functional programming. We define an Interpreter class and implement methods to evaluate each type of expression within the class. To call the correct method, we use conditional statements.

class Interpreter {
	
	String interpret(Expr expr){
		Object value = evaluate(expr);
		return value.toString();
	}
	
	private Object evaluate(Expr expr) {
		if (expr instanceof Binary){
			return evaluateBinary(expr);
		} else if (expr instanceof Grouping) {
			return evaluateGrouping(expr);
		} else if (expr instanceof Literal) {
			return evaluateLiteral(expr);
		}
		
		return null;
	}
	
	private Object evaluateBinary(Expr expr){}
	private Object evaluateGrouping(Expr expr){}
	private Object evaluateLiteral(Expr expr){}

}

This implementation is, in my opinion, a bit better than the OOP one (for this use case). The methods are kept within the relevant classes and separated from the data they operate on, fitting into the functional programming philosophy. Implementing this way allows us to have many different domains (e.g. Interpreter, ASTPrinter and TypeChecker) operate on each type of expression while keeping our code modular.

There are two main “issues” with the approach though

1. It’s inconvenient to add a new Expr type. We only have Binary, Literal and Grouping in Explanck. If we were implementing a fully-fledged interpreted language, we’d care about unary expressions, logical expressions, etc. For every new expression that’s added:
   • we’d need to extend the if-else statements to check for the new expression type
   • and implement a new method to handle the expressions in every domain that exists
2. The if-else statements make for a linear check (i.e. O(n), where n = the number of expression types). This isn’t a problem for a small number of calls, but consider that scripting languages (especially when using their interactive consoles) go through the interpretation process frequently. Remember, slow code (in different places) adds up to make a slow language :)

Let’s see if we can do “better”.

Visitor Pattern 🔗

To address the problems we noted in the last two implementations, we’ll use a design pattern called the Visitor pattern. The Visitor pattern is a behavioural design pattern that lets you separate algorithms from the objects on which they operate¹ and handles the problem of inconvenient conditionals using dynamic dispatch².

To explain the Visitor pattern, let’s write some code. First, we define a Visitor interface:

interface Visitor {
	private Object visitBinaryExpr(Expr expr)
	private Object visitGroupingExpr(Expr expr)
	private Object visitLiteralExpr(Expr expr)
}

Then, we define an abstract Expr class as before. However, this time we add an accept() method in each expression class that accepts a visitor.

abstract class Expr {
	abstract <R> R accept(Visitor<R> visitor);
	
	class Binary extends Expr {
		<R> R accept(Visitor<R> visitor) {
			return visitor.visitBinaryExpr(this);
		}
	}

	class Grouping extends Expr {
		<R> R accept(Visitor<R> visitor) {
			return visitor.visitGroupingExpr(this);
		}
	}

	class Literal extends Expr {
		<R> R accept(Visitor<R> visitor) {
			return visitor.visitLiteralExpr(this);
		}
	}
}

In the Visitor pattern, a Visitor is any behaviour you want to introduce to a collection of objects. In our case, we want to interpret a collection of expressions that the parser has returned, making Interpreter a Visitor. ( If TypeChecker and ASTPrinter existed, they’d be visitors too.)

We then make Interpreter a visitor by extending the Visitor interface. Since Interpreter is now a Visitor, it needs to implement all the methods that Visitor defines: visitBinaryExpr, visitGroupingExpr, and visitLiteralExpr. You’ll notice that these cater to each of our expression types.

Furthermore, in the Interpreter class, we add an evaluate method that calls the accept method of an Expr. Dynamic dispatch determines the correct expression’s accept() method to call at runtime.

class Interpreter extends Visitor<Object> {
	
	String interpret(Expr expr){
		Object value = evaluate(expr);
		return value.toString();
	}
	
	private Object evaluate(Expr expr) {  
		return expr.accept(this);  
	}

	@Override  
	public Object visitLiteralExpr(Literal expr) {}
	@Override  
	public Object visitGroupingExpr(Grouping expr) {} 
	@Override  
	public Object visitBinaryExpr(Expr.Binary expr) {} 
}

And this is where it gets interesting. As we see above, in each expression’s accept() method, it in turn calls a corresponding visitor method: visitor.visitBinaryExpr() for Binary expressions, visitor.visitGroupingExpr() for * Group* expressions and visitor.visitLiteralExpr() for *Literal* expressions.

This is how the correct method to process an expression is resolved using the visitor pattern. It is better than OOP because we don’t have to mix domains with data. Also, it is better than the FP implementation in the last section because it doesn’t need a linear check to determine the correct method to evaluate an expression - dynamic dispatch happens in constant time.

Let’s walk through an example to solidify our understanding here.

Suppose we had the expression: 9. After scanning and parsing, we get an AST that can be visualized as:

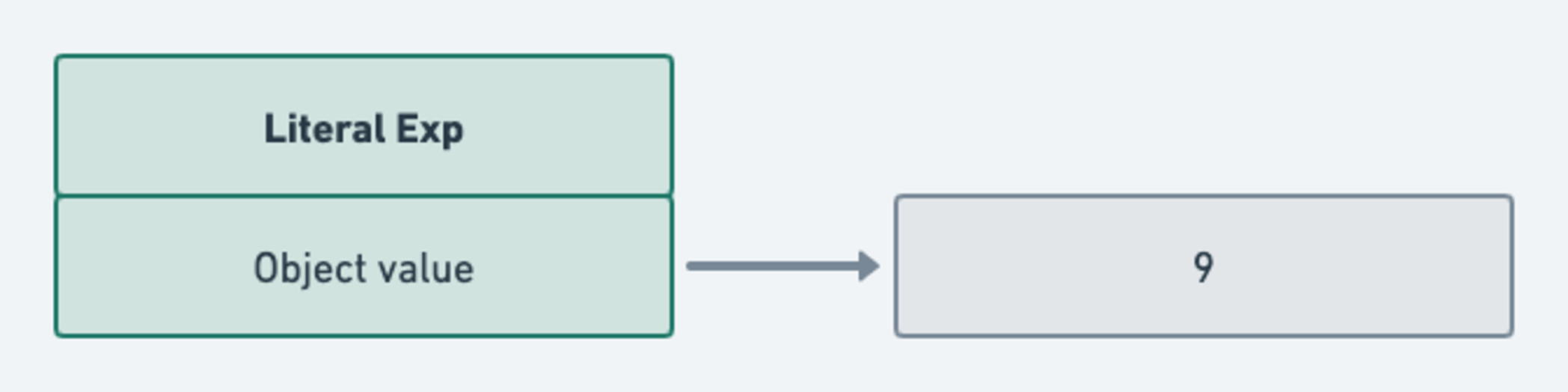
The “object” form can be written as: Literal(value: 9). This is a literal expression, and we need to interpret it to get our final value.

Expr expr = Literal(value: 9);
String result = new Interpreter().interpet(expr);

And this is a visual of what happens next:

See the full image here .

In short, since this is a literal expression, the accept() method in the Literal class is called. This, in turn, calls the visitLiteralExpr() method in the Interpreter class, which outputs the final result: 9.

That’s how the Visitor pattern works - there might be slight variations in different mediums, but this covers the main gist. Before we go, let’s implement each visit method in Interpreter.

For visitLiteralExpr, all we need to do is return the object’s value.

@Override  
public Object visitLiteralExpr(Literal expr) {  
	return expr.value;  
}

For visitGroupingExpr, we evaluate the expression within the Grouping expression. Remember that a grouping expression is an expression wrapped in parentheses, so all we need to do here is evaluate the expression within.

@Override  
public Object visitGroupingExpr(Grouping expr) {  
	return evaluate(expr.expression);  
}  

The visitGroupingExpr method is a bit more involved. Binary expressions are of the form left_operand operator right_operand. So we need to check what the operator is for the different operators we care about and then use Java to perform the operation.

@Override  
public Object visitBinaryExpr(Expr.Binary expr) {  
    Object left = evaluate(expr.left);  
 	Object right = evaluate(expr.right);  
  
	 switch (expr.operator.type) {  
		case MINUS:  
			return (double) left - (double) right;  
		 case PLUS:  
			return (double) left + (double) right;
		case SLASH:  
			return (double) left / (double) right;  
		 case STAR:  
			return (double) left * (double) right;  
		 case POWER:  
			return Math.pow((double) left, (double) right);  
	 }  

	return null;  
}

And that is it, our interpreter lives! We can now do this:

String exp = "120 + 12.3 * 53 - 9";
List<Token> tokens = new Scanner(exp).scanTokens(); //[NUMBER 120, PLUS, NUMBER 12.3, STAR, NUMBER 53, MINUS, NUMBER 9]

Expr expr = new Parser(tokens).parse(); // Binary(Binary(120, PLUS, Binary(12.3, STAR, 53)), MINUS, 9);

String result = new Interpreter().interpet(expr) // 762.9

Conclusion 🔗

This brings us to the end of the explanck series. It was a lot longer than I had initially planned, but we achieved our goal - we have built an expression evaluator.

I’ve built a small client for the evaluator that you can play with online, and you can find the complete explanck project on GitHub.