In this series' last post, we discussed the threat of ambiguous grammars for math expressions, and we generated an unambiguous grammar for explanck. In this post, we will write a parser based on our grammar.

The main goal of our parser is to generate an abstract syntax tree from the sequence of tokens returned by our tokenizer¹. While many parsing algorithms are available ², we will focus on a type called Recursive Descent Parsing in this post.

Recursive Descent Parsing 🔗

Let’s remind ourselves of the grammar again:

expression -> term
term -> factor (("+" | "-") factor)*
factor -> power ((" * " | "/") power)*
power -> primary ("^" primary)*
primary -> NUMBER | "(" expression ")"

Recursive descent is a top-down ³ parser that associates each rule name (a.k.a non-terminal) in our grammar with a function. It is called top-down because it goes from the lowest precedence rule (expression, in our case) to the highest precedence rule (primary, in our case).

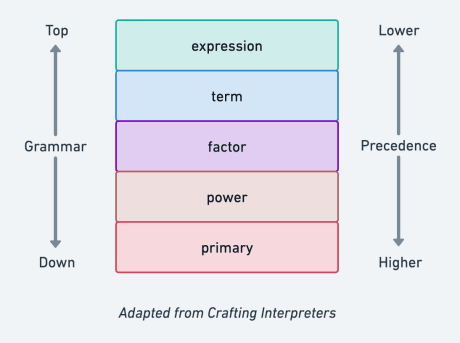
As we implement the parser, keep the following in mind wrt to explanck’s grammar above:

• Each non-terminal is a separate method, and each method produces an abstract syntax tree and returns it to the caller
• | means “or” which means we must choose from multiple options. In our code, we will make this choice in an if statement
• (...)* means zero or more of whatever is within the parentheses. We will represent this using a while loop, with the while loop’s condition enforcing the “zero or more” part

Okay, let’s begin implementation.

First, we define a Parser class that accepts a list of tokens in its constructor and keeps track of the last token that has been processed.

and implement the logic for the two lowest precedence rules: expression and term.

class Parser {
	// Tok keep track of processed tokens.
	private int current = 0;
	Parser(List<Token> tokens){}
}

According to the grammar, expression simply expands to term, so in our code we return term() in expression().

// In Parser.java
private Expr expression(){
	return term();
}

term is a little more interesting. Remember that term’s rule is term -> factor (("+" | "-") factor)*. The first * factor* non-terminal translates to a call to the factor(). Then the (...)* part of the body means a while loop. Within (...)*, we have two parts: ("+" | "-") and factor.

The first part - ("+" | "-") - represents the condition that must be met for the block of code within the while loop to execute. That is, the block of code within the while loop will continue to execute as long as the next token in our expression is “+” or “-”.

And the second part - factor - represents the code that will execute within the while loop as long as the condition is met.

// In Parser.java
private Expr term(){
	Expr expr = factor();

	while(nextToken(TokenType.MINUS) || nextToken(TokenType.PLUS)){
		Token operator = previous();
		Expr right = factor();
		expr = new Binary(expr, operator, right);
	}
}

// Checks if the next token is a particular token type
private boolean nextToken(TokenType type){
	if (!isAtEnd()) return false;

	if (tokens.get(current).type == type) {
		current++;
		return true;
	}

	return false;
}

private Token previous(){
	return tokens.get(current - 1); 
}

Once we enter the while loop in term(), we know that we are parsing a term expression (i.e. an expression with “+” or “-"), so the call to factor() within the loop is to resolve the right operand of the expression. Once we determine the right operand, we create a new Binary expression.

The while allows us to keep checking for term operators as long as they exist, making it possible to handle expressions like 2 + 3 - 5, which contains more than one term operator. After creating a Binary object for 2 + 3 like Binary(2, PLUS, 3), the while loop will keep checking and find - and then resolve the right operand: 5. Our final object will be Binary(Binary(2, PLUS, 3), MINUS, 5).

One important thing to note here is that even if we get an expression like 2 * 3 with no term operator, term() will still resolve this expression by calling the first factor(). In this way, term() can resolve term expressions or any other expressions with higher precedence. This is what I meant in the last post by “each rule will only match expressions at their precedence level or higher” .

The logic for factor and power looks very similar to term. The only differences are the operators we check for in the while loop’s condition and the methods we call to resolve the left and right operands.

// In Parser.java
private Expr factor(){
	Expr expr = power();

	while(nextToken(TokenType.STAR) || nextToken(TokenType.SLASH)){
		Token operator = previous();
		Expr right = power();
		expr = new Binary(expr, operator, right);
	}
}

private Expr power(){
	Expr expr = primary();

	while(nextToken(TokenType.POWER)){
		Token operator = previous();
		Expr right = primary();
		expr = new Binary(expr, operator, right);
	}
}

Lastly, we implement the rule for primary.

// In Parser.java
private Expr primary(){
	if (nextToken(NUMBER)) {
		return new Literal(previous().literal);
	}

	if (nextToken(LEFT_PAREN)) {
		// We start from the root expression again
		Expr expr = expression();
		
		if (!nextToken(RIGHT_PAREN)){
			// throw error
		}
		
		return new Grouping(expr)
	}
}

I’ve separated primary’s code because it looks slightly different from the others. primary’s rule is primary -> NUMBER | "(" expression ")". So, the first thing we do in the code is check if the next token is a number. If it is, we create a Literal expression out of it and send it back up the call stack.

If we don’t find a number, we possibly have a grouping expression - expressions wrapped in parentheses. So, we look for ( and then evaluate the inner expression by calling expression() again :). This call makes this tree indirectly recursive, hence the “recursive” in “recursive descent”.

We have all the parts of our parser now, and we can call it like so

// In Explanck.java
Expr expr = new Parser(tokens).parse();

Okay, so we have our parser. Let’s take a few examples to understand how it works. You might need a pen ;).

Expression: “120” 🔗

We get [NUMBER 120] back from the scanner, initialize our parser with that and call parse().

// In Explanck.java
String exp = "120";
List<Token> tokens = new Scanner(exp).scanTokens(); // [NUMBER 120]
Expr expr = new Parser(tokens).parse();

Here’s a diagram detailing the parsing steps:

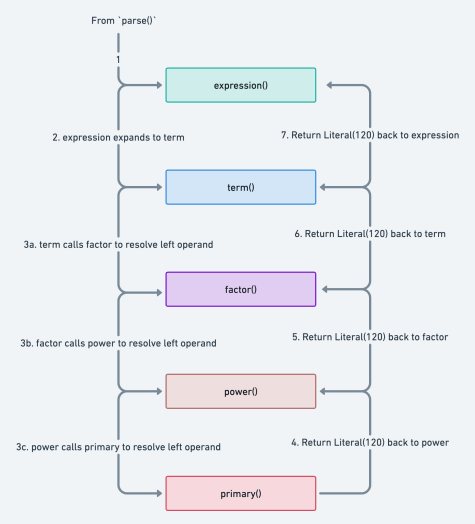
See image in full screen here .

In the diagram above, we walk down each rule’s method in order of precendence: expression() -> term() -> factor() -> power() -> primary(). The expression is a number which gets evaluated in primary() and returned up the stack back to the caller.

So, our final AST is:

Expression: “53 - 9” 🔗

We get [NUMBER 53, MINUS, NUMBER 9] back from the scanner, initialize our parser with that and call parse().

// In Explanck.java
String exp = "53 - 9";
List<Token> tokens = new Scanner(exp).scanTokens(); //[NUMBER 53, MINUS, NUMBER 9]
Expr expr = new Parser(tokens).parse();

Here’s a diagram detailing the parsing steps:

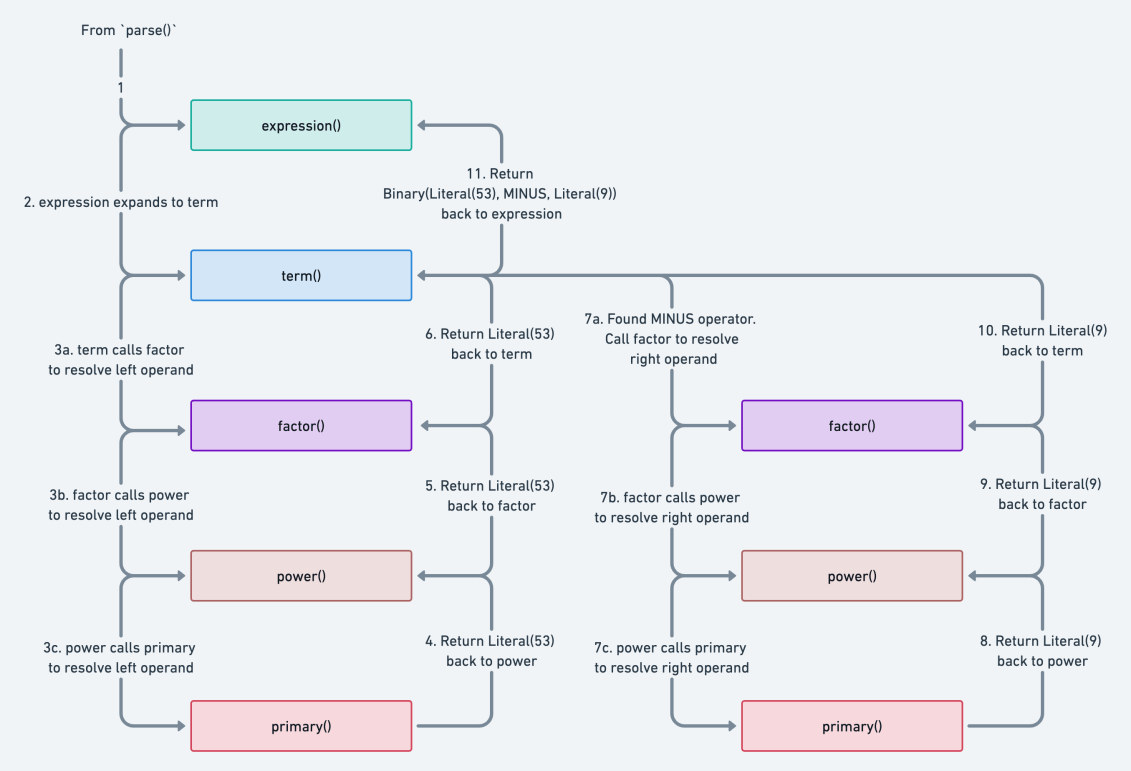
See image in full screen here .

This expression is more complex than the first example because it contains more than one operand and an operator. So, firstly we walk down each rule’s method from expression() to primary() to resolve 53 as a literal expression (i.e. Literal(53)).

As we return this literal expression up the stack, we eventually get back to term(), where we realize that the symbol in the next index is a subtraction operator. It is term()’s job to resolve term expressions, so it does exactly that.

We resolve 53 - 9 to a binary expression containing two literal expressions (as left and right operands) and a subtraction operator.

In the end, our AST looks like this:

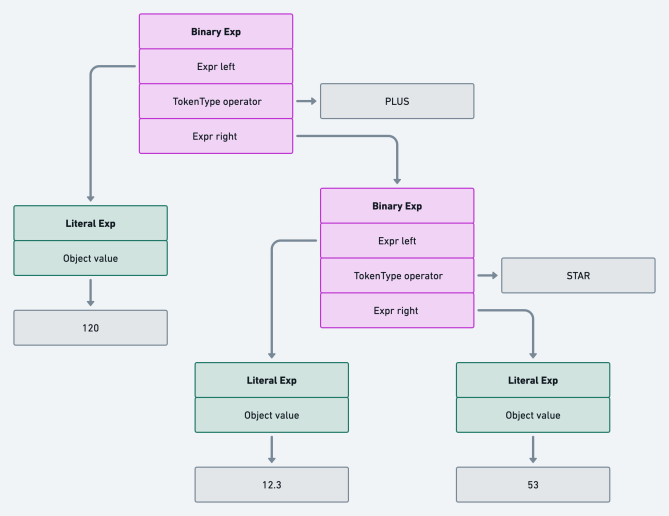
Expression: “120 + 12.3 * 53” 🔗

Let’s take a final example to highlight precedence.

For the expression above, we get [NUMBER 120, PLUS, NUMBER 12.3, STAR, NUMBER 53] back from the scanner, then we initialize our parser with that and call parse().

// In Explanck.java
String exp = "120 + 12.3 * 53";
List<Token> tokens = new Scanner(exp).scanTokens(); //[NUMBER 120, PLUS, NUMBER 12.3, STAR, NUMBER 53]
Expr expr = new Parser(tokens).parse();

Here’s a diagram detailing the parsing steps:

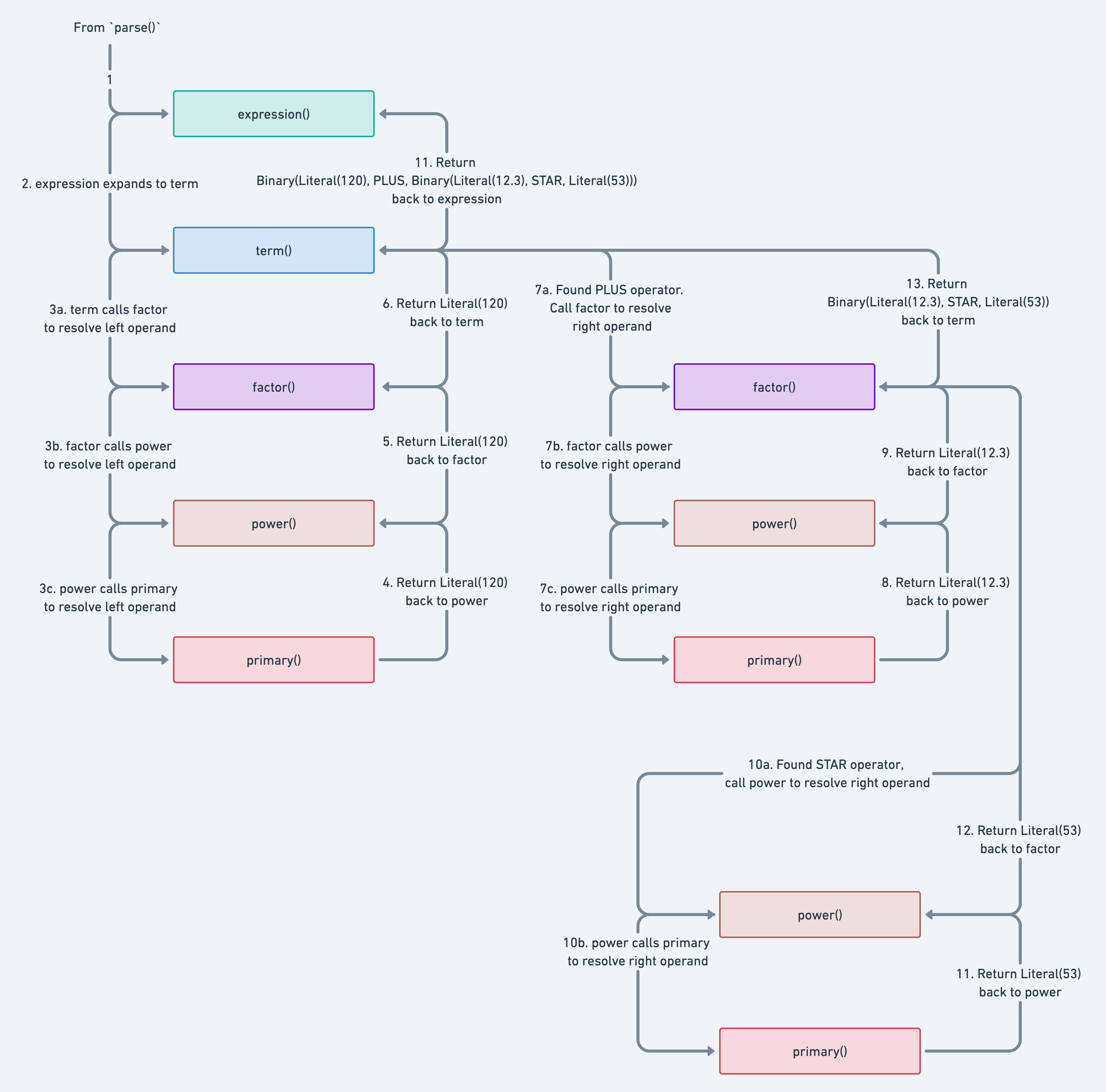
See image in full screen here.

This final example is the most complex of our examples so far. As you’ll have noticed, it contains a multiplication operator placed after an addition operator (when reading the expression L-R). We know from precedence rules that we must resolve multiplication before addition; this example is essential to help you see that in practice.

The parsing image above does an excellent job of showing a step by step process to resolve the expression, but let’s summarize quickly.

First, we go from expression() to primary() to resolve 120 as a literal expression. As we return 120’s literal expression up the stack, we realize at term() that the next symbol is an addition operator, so we try to resolve the right operand, but it doesn’t happen as one might guess.

We walk down from term() to primary() to resolve 12.3 as a literal expression. However, as we return 12.3’s literal expression up the stack, we realize at factor() that the next symbol is a multiplication operator, so we go back down from factor() to primary() to resolve the right operand for the factor expression.

So, at the end of the day, what term() gets back as a right operand isn’t 12.3’s literal expression, but a factor expression made up of literal expressions (for 12.3 and 53) and a multiplication operator.

The fact that we resolve a factor expression before a term expression (that’s already in flight) is how we ensure precedence in our parser!

In the end, the AST looks like this:

Conclusion 🔗

When I first read about recursive descent parsing, I found it thoroughly elegant - it uses recursion and an idea borrowed from post-order traversal to enforce precedence. I hope this was fun!

We will use post-order traversal directly to walk through our abstract syntax tree to generate our result in our next and final post. Along the way, you’ll learn about a design pattern :). See you in the next one.

In the meantime, you can find the code of the parser on GitHub!